La trasformata di Laplace è una operazione che si esegue sulle funzioni a variabile reale per trasformarle in funzioni a variabile complessa.
Questa operazione, contrariamente a quello che si può pensare, consente di apportare notevoli semplificazioni nei calcoli matematici.
Facciamo considerazioni solo su funzioni del tempo che sono quelle più ricorrenti nello studio dei fenomeni fisici; quindi il tempo viene considerato come variabile reale, indipendente, e le sue funzioni f(t) vengono definite per t>0 considerando nulle le f(t) per t<0.
Indichiamo con s la variabile complessa s=σ+jω (pulsazione complessa) e con F(s) la funzioni a variabile complessa.
Data una funzione f(t) reale e nulla per t<0, si definisce trasformata di Laplace della f(t) e la si indica con: $F(s) = L[f(t)]$ la seguente funzione
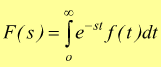
dove s=σ+jω è la pulsazione complessa.